Koch Snowflake

Overview of Algorithm

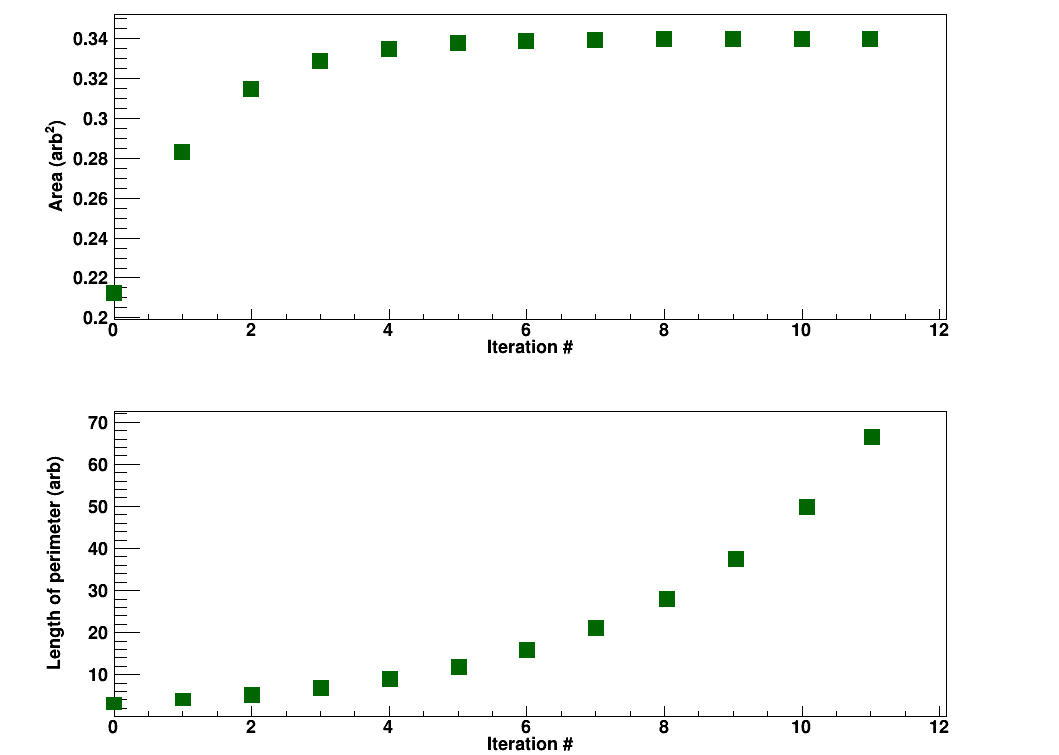
I worked on this project immediately after the tree fractal. Admittedly, the geometry is more difficult but the fractal generation concept is the same; find a base operation, and apply it iteratively. The fractal begins by defining an equilateral triangle, and let's refer to this as iteration 0. Iteration 1 is formed by taking each line segment making up the base triangle, splitting it into thirds, removing the center segment, and then building a smaller equilateral (with one side missing) with two additional line segments. The result is a star. Therefore, the base operation of the fractal consists of accepting one line segment and returning four in the proper orientation. Repeat the iteration process until satisfied, but practically only the first 6 iterations or so make noticeable changes without magnification. An animation of my Koch snowflake may be seen by Fig. 2. The area of the fractal quickly converges, but the perimeter tends towards infinity; see Fig. 3 for my results. Note that the number of line segments to consider grows rapidly: 3*4ⁿ where n is the iteration number. Therefore, the animation displays the first 10 iterations resulting in a fractal with 3.14*10⁶ line segments.