Mona Lisa
A hill climbing method to mimic an input image with randomly generated triangles

Disclaimer: I got the idea from this blogging site, but the implementation/algorithms are mine. The blogger calls this a "genetic algorithm" but it's just a simple hill-climbing method defined by some χ2, a common technique in my work. Additionally, I used the bare-bones SFML library which required significant image processing and filtering methods to be developed; this has been done on purpose for my own education! While the results are pleasing, the algorithm is not practical (at least mine). An animation of the algorithm is located at the bottom.
Concept

The goal is to mimic or replicate an input image using polygons, or triangles in this case. The main components of the algorithm are as follows:
- Have an input image that we wish to copy, e.g. the Mona Lisa
- Randomly generate an initial set of N triangles, typically 50-500
- Define an appropriate χ2 function, often referred to as a loss or fitness function, which will allow us to quantify the difference between the triangle image and the input image
- Apply a
mutation
, i.e. randomly tweak a characteristic of the triangle like a vertex coordinate or an RGBA value - Calculate the χ2 between the mutated image and the input; if the function determines that the mutation is more similar to the input then accept the change. Otherwise, discard it, and apply another mutation
- Repeat until the loss function does not change significantly.
With low-level C++ libraries, the difficulty here is to develop the appropriate routines to handle the image processing. For example, N triangles are randomly generated in which there is significant overlap; therefore, RGBA values are being added together in a complicated manner. While more sophisticated methods can be developed, I chose to draw the triangles on a canvas in order to visually see the result of a mutation (for example, a coordinate mutation can affect a significant fraction of the RGBA of the mutation image). In order to process the mutated image, the code takes a screen shot of the mutation and then breaks it apart into a vector such that the RGBA components may be easily compared to the input image.
Let's define the word mutation clearly. A mutation only applies to the triangle image, and in general represents some random tweaking of triangle attributes. In this case, one triangle has three vertices and each vertex has two coordinates and an RGBA value; this is 6 parameters per vertex for a grand total of 18 per triangle! Therefore, the number of parameters to tweak making up the triangle image goes like N*18 where N is the number of triangles. The difficulty is to decide how much to randomly tweak a parameter. If the mutation is too small then it is easy for the code to get stuck in a local minima, but if it is too large then the mutation rate is compromised. I used a flat random number generator for all parameters, and kept the coordinate mutations loose while keeping tight mutations on the color components. There is a lot of room for improvement in these choices, I think.
The χ2 function is defined to be the square difference of R,G,B,A components for all pixels between the input and mutated image, and is normalized by (N pixels)*4*256*256 such that the loss function L = 1-χ2 yields a number less than or equal to 1 where 1 is a perfect match. This can be computationally slow if you have large images as the code is simply brute force. The heart of the algorithm depends on this function as the newly mutated image gets compared to the input image via the loss function. If the loss function is calculated to be better than the previous triangle image, then the mutation is kept; otherwise, the code will discard the mutation and randomly try again. The mutation rate, i.e. the number of accepted mutations over the total number of mutation attempts, at first is acceptable but then quickly becomes linear resulting in a slow algorithm (still fun though).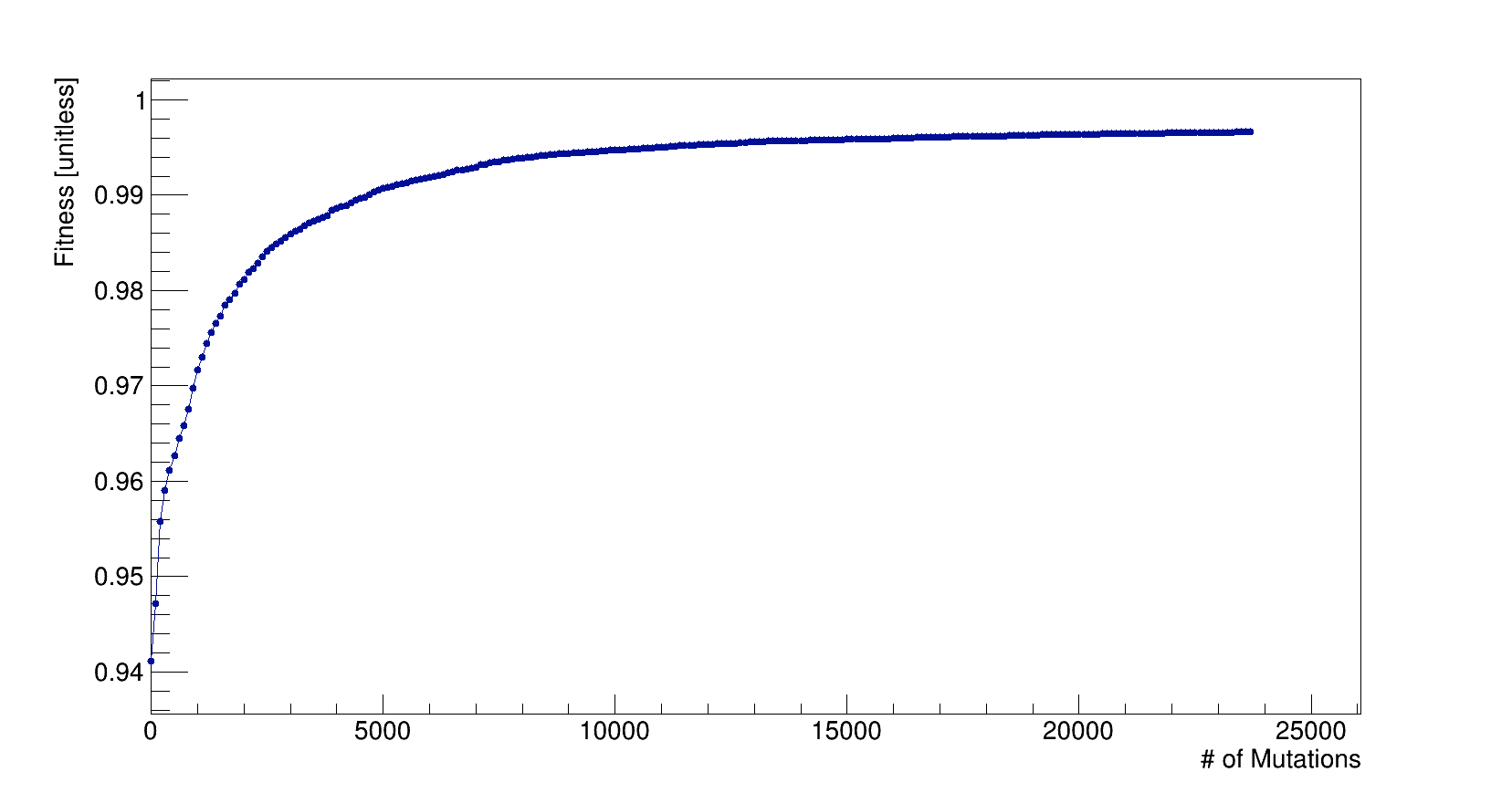
Results

In order to make convergence faster, I gridded up the input image and found the average color of each grid. I generated 300 triangles with randomly placed vertices and calculated the vertex coordinate average which dictates the triangle's initial color based off the average grid colors. I let the code do 1e6 mutation attempts (as opposed to successes) in which only 23,721 mutations were accepted, which is a mutation rate of 2.4% if I assume linearity. The best loss is L=0.9966, and it remained this way for quite some time as the slope is so small (see Fig. 1 at large mutations). The quality of the image does converge, meaning that more computational time is most likely futile. The results may be greatly improved by considering polygons (I've seen ellipses too), but the number of parameters to tweak is now N*V*6 where V is the number of vertices. Also, the use of triangles leads to sharp edges in the output image. This can be smoothed out by developing filtering techniques, e.g. a Gaussian blur, and I spent a great deal of time learning how to apply convolution matrices or image masks (google 'kernel image processing') from scratch.