Self-Avoiding Walk

Overview

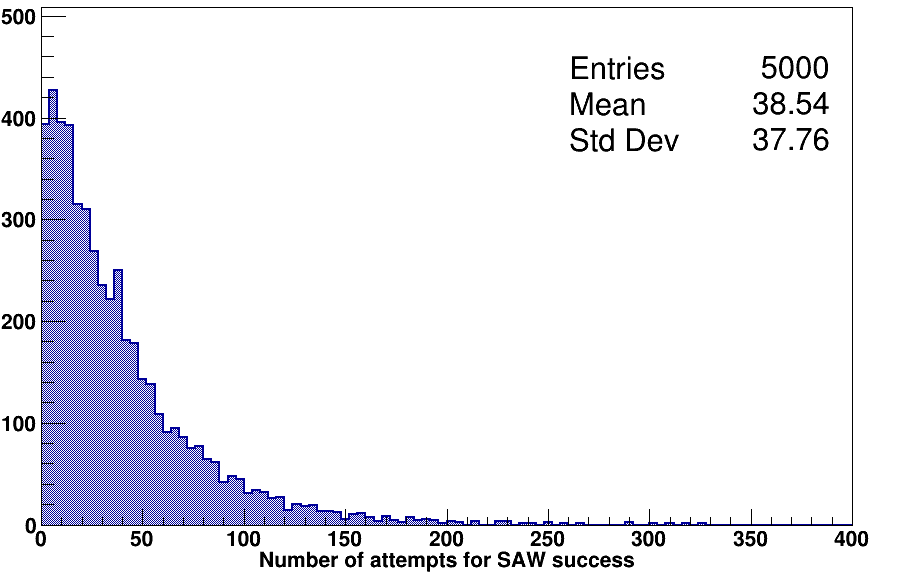
Over the years, I have simulated many random walks, e.g. one to three dimensional drunkards, plinko, gaussian random walks, and brownian motion to name a few; the phenomenon is ubiquitous in physics. The self-avoiding walk (SAW) is a nice spin-off of the 2D random walk and results in pictures that are reminiscent of a maze. The idea is to randomly traverse a lattice without returning to an already visited node; therefore, all lattice nodes must be touched once (no more and no less) in order for the walk to be a success. The walker only moves in the vertical and horizontal directions so only four directions need to be considered. For efficiency, a table that maps each node to a list of its nearest neighbors (four neighbors is max) is constructed. The algorithm then starts in the top left corner and generates a random move. Two algorithms have been considered. First, when a node has been visited, it is removed from the list of neighbors and will not be considered in subsequent maneuvers. Second, no node removal is done, and if the walker hits a previously visited node then the walker must start over. For the remainder of this post, though, I will discuss the former. If the random walker touches every node, then the simulation is said to be a success. On the other hand, if the random walker encounters a situation when no neighbors are available then the simulation is a failure. The algorithm is very inefficient for large lattices due to the nature of random numbers and the number of possible paths (which can be calculated with knowledge of binomial/combinatorics). The distribution of attempts needed for a success with a 5x5 lattice may be seen within Fig. 2 which includes 5,000 SAW simulations. The exercise has been repeated for 6x6 resulting in a similar distribution in shape with a significantly larger spread (mean and standard deviation jumps to roughly 360 and 350, respectively). See this paper for really cool information on the subject and how they may be used in physics.