Tree Fractal

Generating and Animating the Fractal

There are many ways to generate a simple tree fractal. A quick google search gives many variations and patterns, symmetric and asymmetric, as even small changes to the initial length and/or angle gives interesting results. I will only describe my fractal as I am not a fractal expert; the goal for me was to generate a symmetric tree fractal, and then to tweak parameters (such as angle) and make an animation.

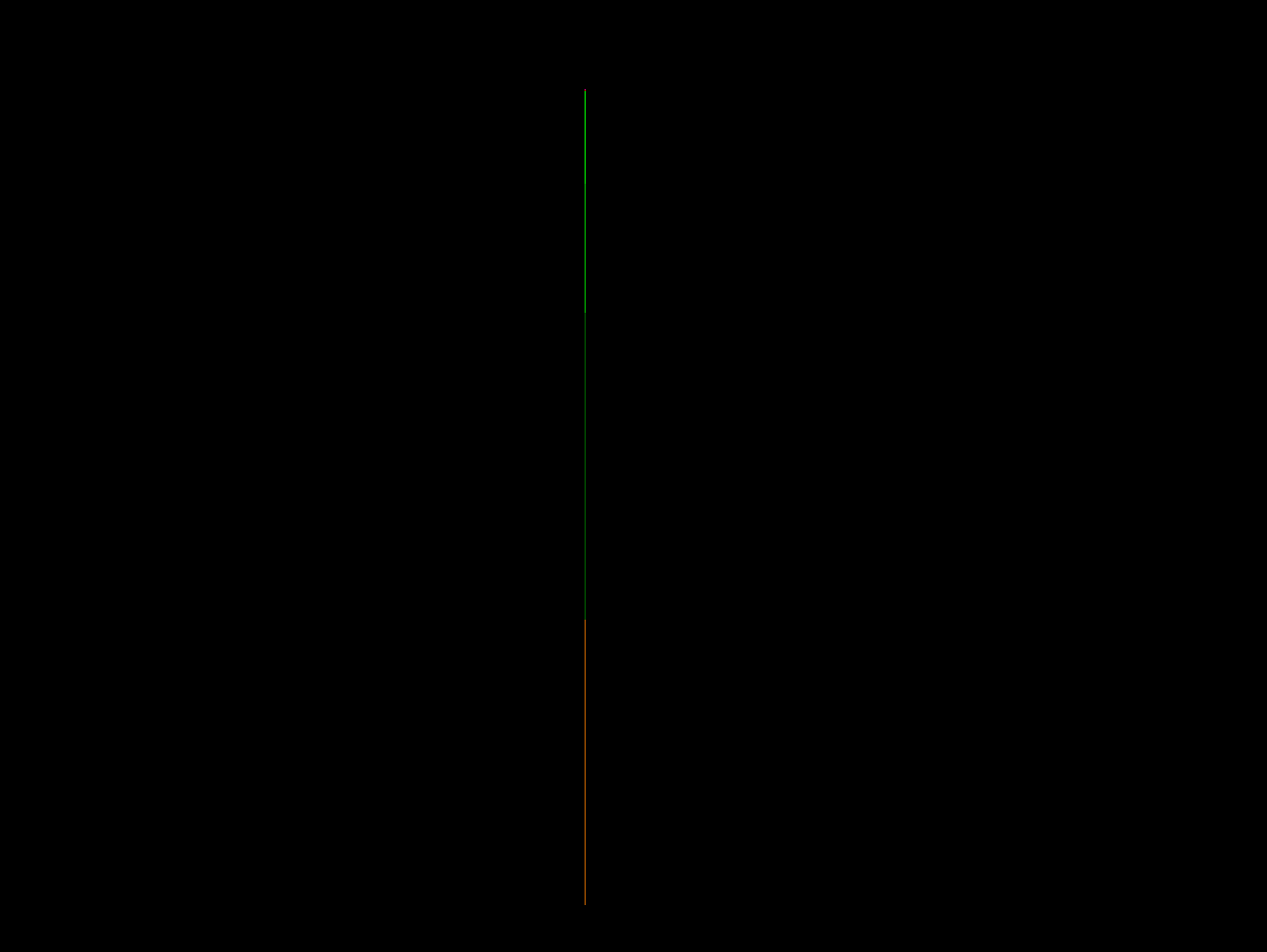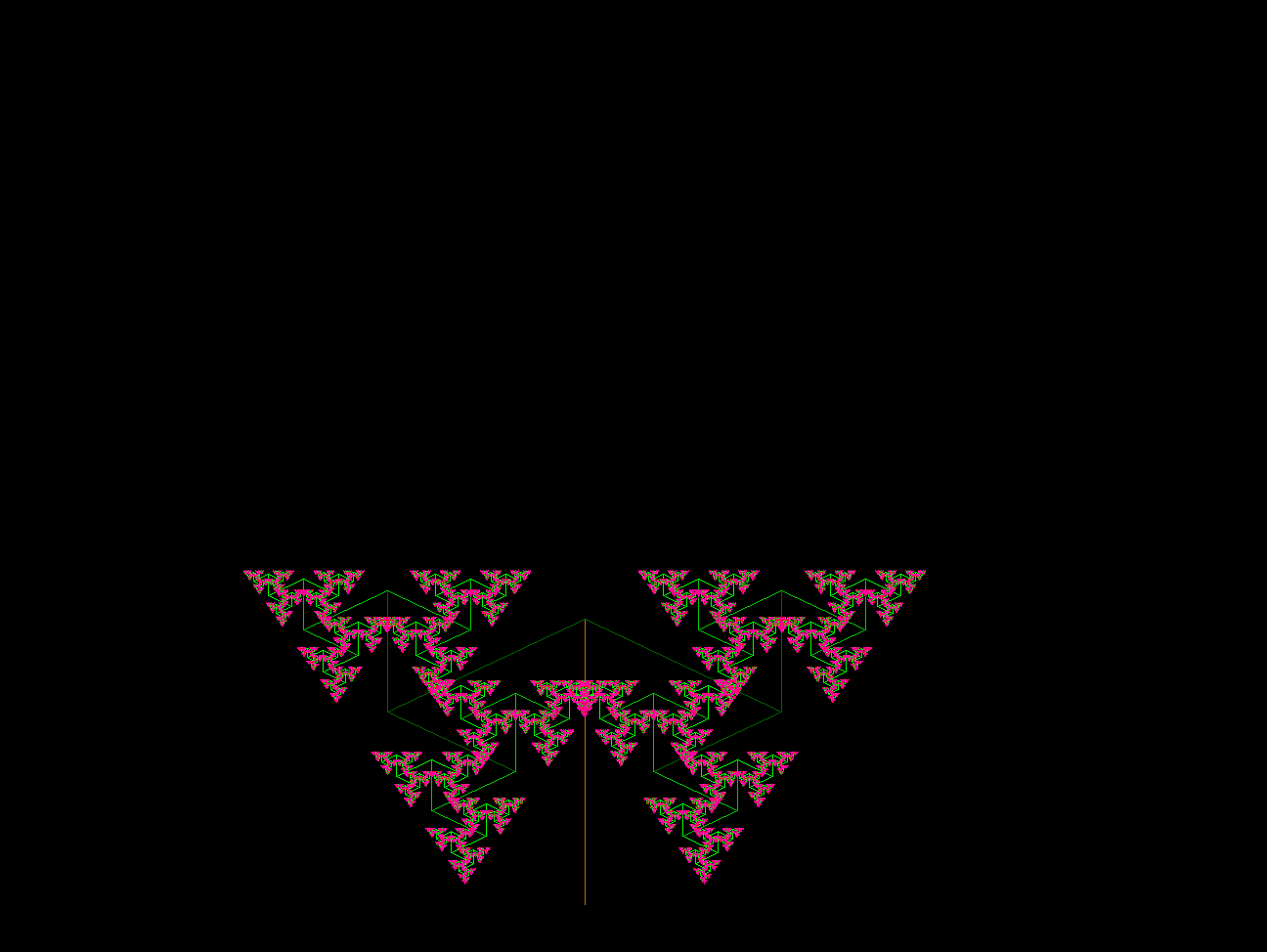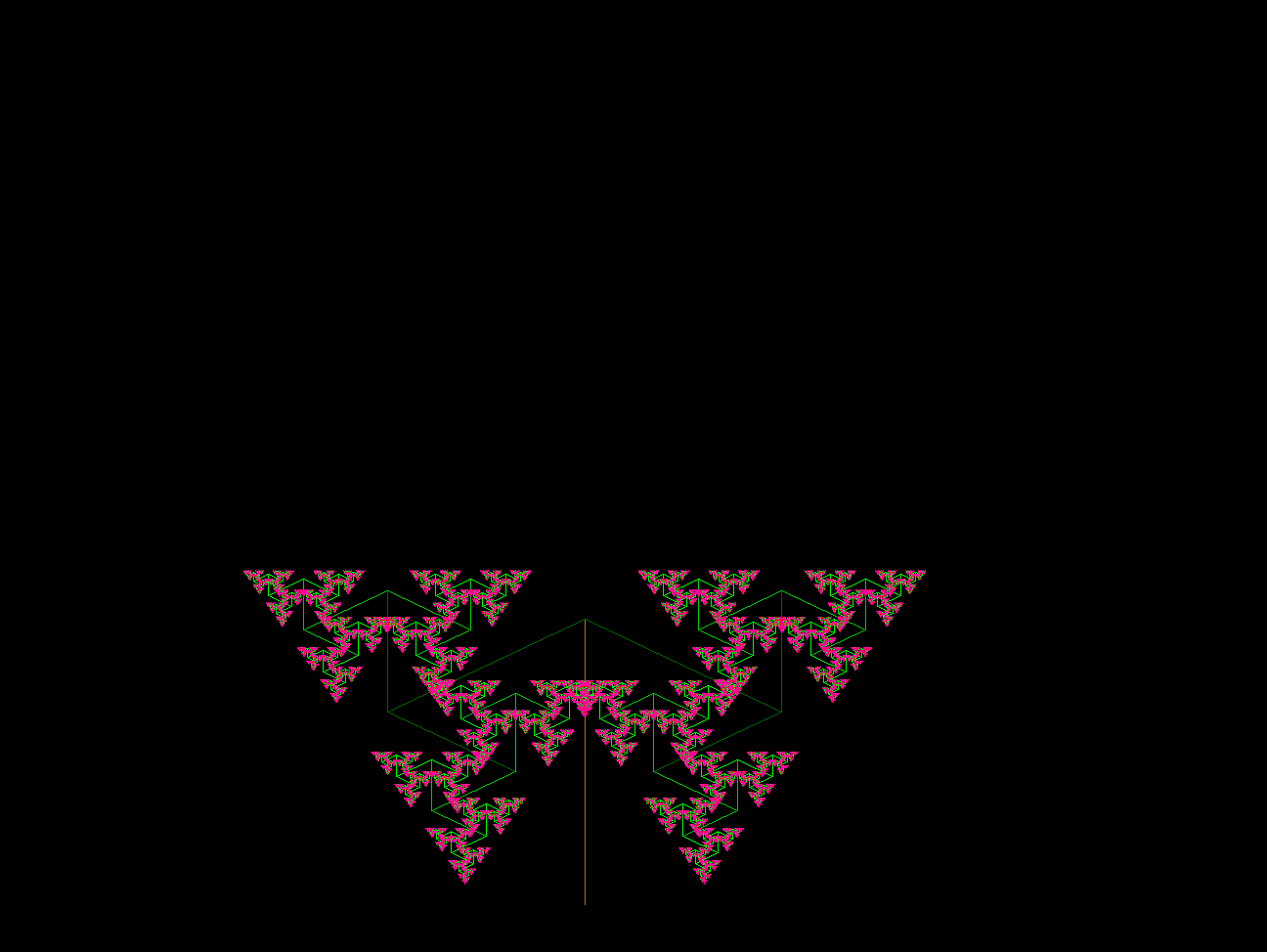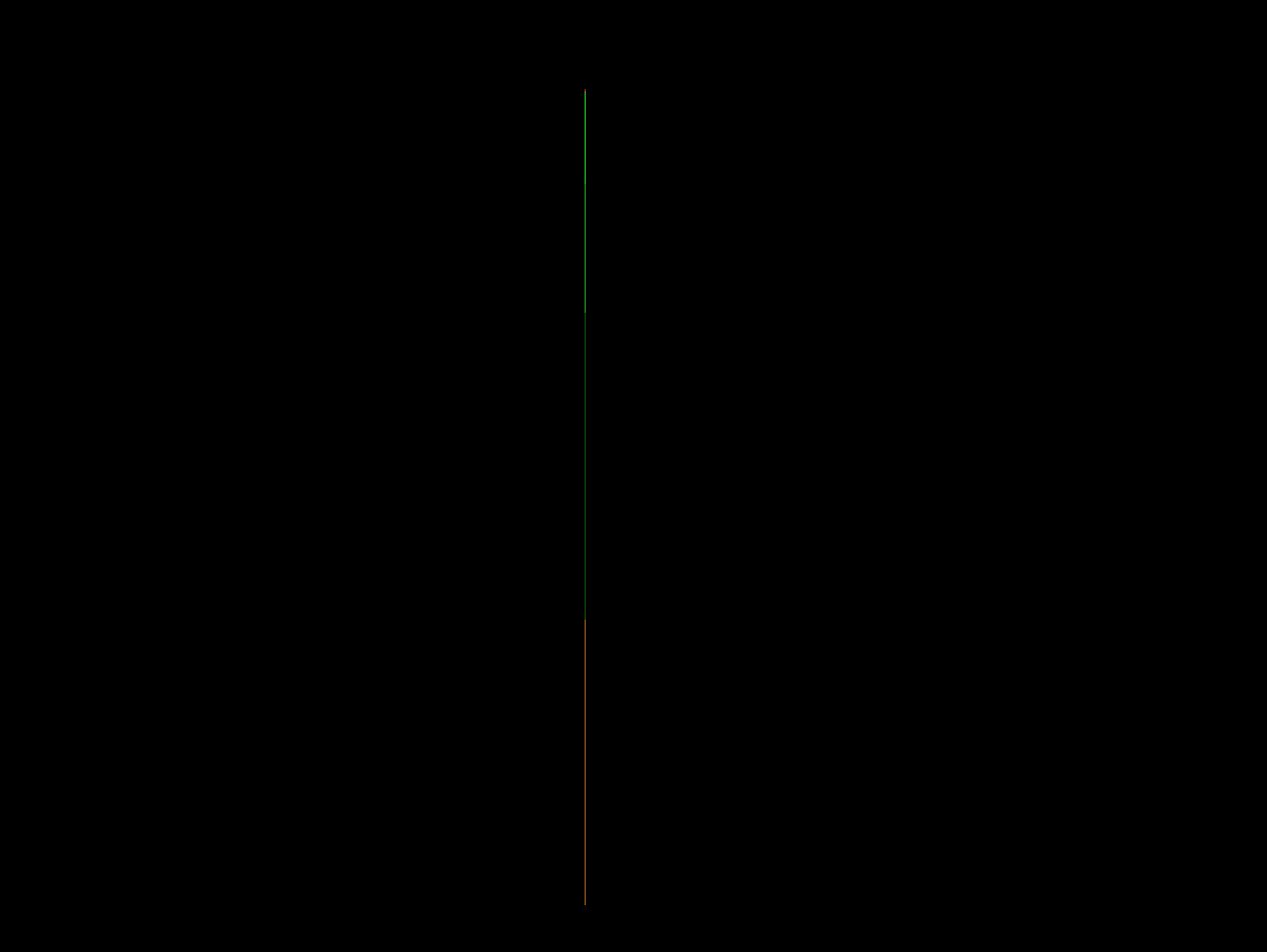
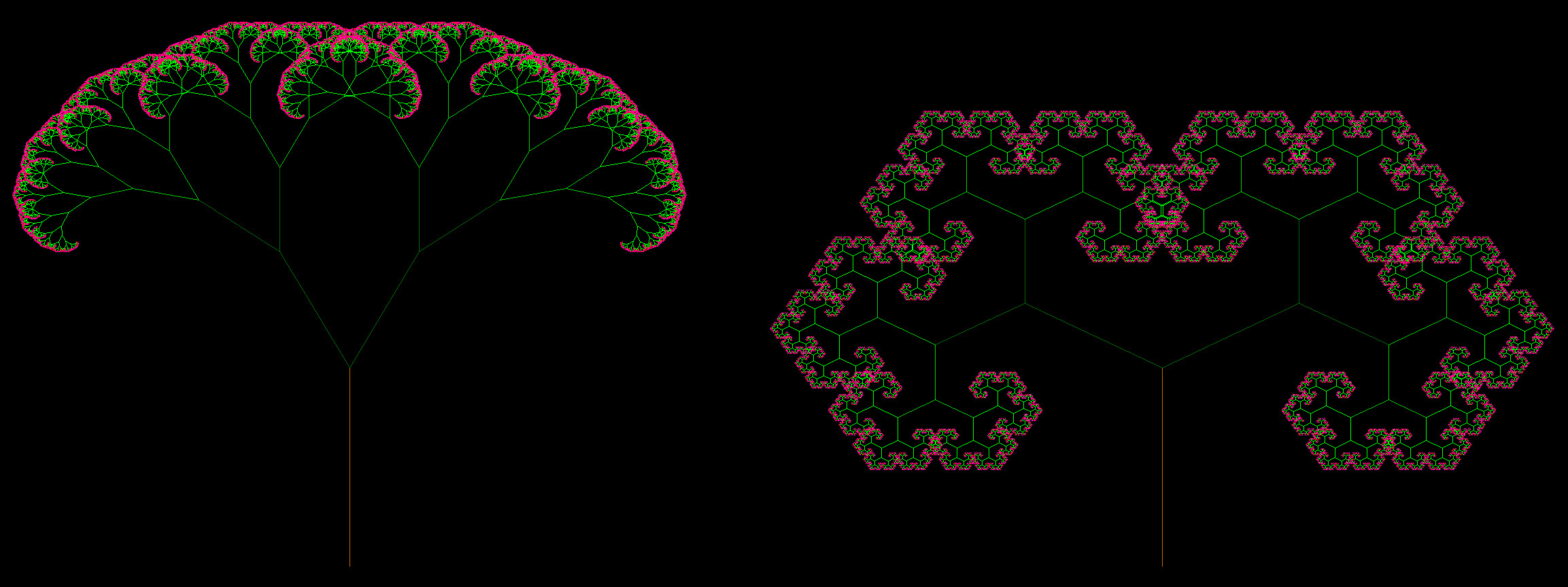
The fractal starts with a tree trunk of length l, and think of the top of the trunk as a node where we will connect branches. Fractals are iterative objects, so in this case the trunk is referred to as level zero. Each time we increment the level, 2 branches will be connected to each node of the previous level resulting in 2ⁿ new branches where n represents the level. A branch is just a line defined by two coordinates. The first level of the fractal, then, generates two branches, both assigned a length al where a is some fraction to be defined by the coder, with the trunk node as the starting coordinate; the end coordinate depends on the fractal generation angle. If I choose an angle of say 23 degrees as in Fig. 1, then the first level branches have end points that are plus/minus 23 degrees with respect to the vertical, or more generally the directional vector of the trunk (or branch of the previous level). Level two branches (there are 2²=4) use level 1 nodes as input where the length is now a²l, and the end points are defined relative to the level 1 branch directional vectors. The process is iterated to as many levels as one wants, but note that the length of level n branches are reduced relative to the trunk by a factor of aⁿ. For example, if we choose a=0.7, then the length of level 7 branches is 0.7⁷=0.08 or 8% of the trunk's length which quickly becomes difficult to visualize. Additionally, the tree fractal naturally gives rise to a curling or rotational effect which yields often unexpected behavior, e.g. the right panel of Fig. 1.

I used a value of a=0.65 and n=15, and incrementally changed the color of branches as the algorithm progresses to higher branch levels, hence the variations of green and the red/pink buds. Obviously a great deal of time could be invested tweaking various parameters and checking the result; the tweaking can be intensified by considering asymmetric parameters for left/right branch generation at any particular node. The algorithm can easily be extended to scan over a range of branch generation angles, say 0 to 360 degrees, and the output can be strung together to create a .gif using conventional linux facilities. The results of such a procedure may be seen by Fig. 2, and if the .gif does not work then see the video on my youtube channel. Fractal analysis can be performed on the output, but I stopped here. See this video for a spectacular demonstration of the variety of tree fractals.