20 May 2018

Random Tree Generator

A significant upgrade to the previous tree fractal post

Fig. 1 - A fractal tree using my "random tree generator" with the black/white option turned ON. The tree has been placed on top of a photograph of the Badlands that I took during a road trip (summer of 2012).

Summary

  1. The tree fractal program may be seen by this video
  2. Improvements relative to original post
  3. Random tree generator
  4. Pretty pictures

Improvements

I realized that I wanted to play with the fractal tree a bit more… My first post may be seen here which includes an overview of the algorithm. The code has been extended/reformulated to handle a variety of options in addition to a GUI interface; this is how the tree gets interesting which I ignored the first time! While I have written sliders, buttons, and number entries from scratch, I used the C++ ROOT GUI widgets for this project which has been an absolute pleasure. Furthermore, instead of simply representing a branch as a line, I included an option to toggle between lines or user-adjustable trapezoids, where the latter is designed to give the effect that the diameter of a branch/trunk decreases with height. The parameters that are now adjustable using GUI widgets are the following:

  1. the number of iterations to display
  2. the number of branches to generate at a particular node (previously I only did 2, but now it is possible to choose between [1,10])
  3. the generation angle which controls the angle of branches in the n+1 iteration relative to the nth iteration
  4. the length and width of the trunk which affects subsequent branches as well
  5. the trapezoidal gradient of a branch
  6. the branch width and length relative to the trunk
  7. an asymmetry angle offset which yields trees that are biased towards one direction
  8. an offset for the starting point of a branch
  9. an option to turn the background back/white which automatically renders the tree white/black, respectively
  10. an option to draw the branches in order/reverse (sometimes branches cover previous iterations, therefore this option is for convenience)
  11. choose between 15 color palettes which automatically applies a color gradient over the trunk to the smallest branches
  12. the ability to randomly generate a tree in which the above parameters are tweaked according to various probability distributions.

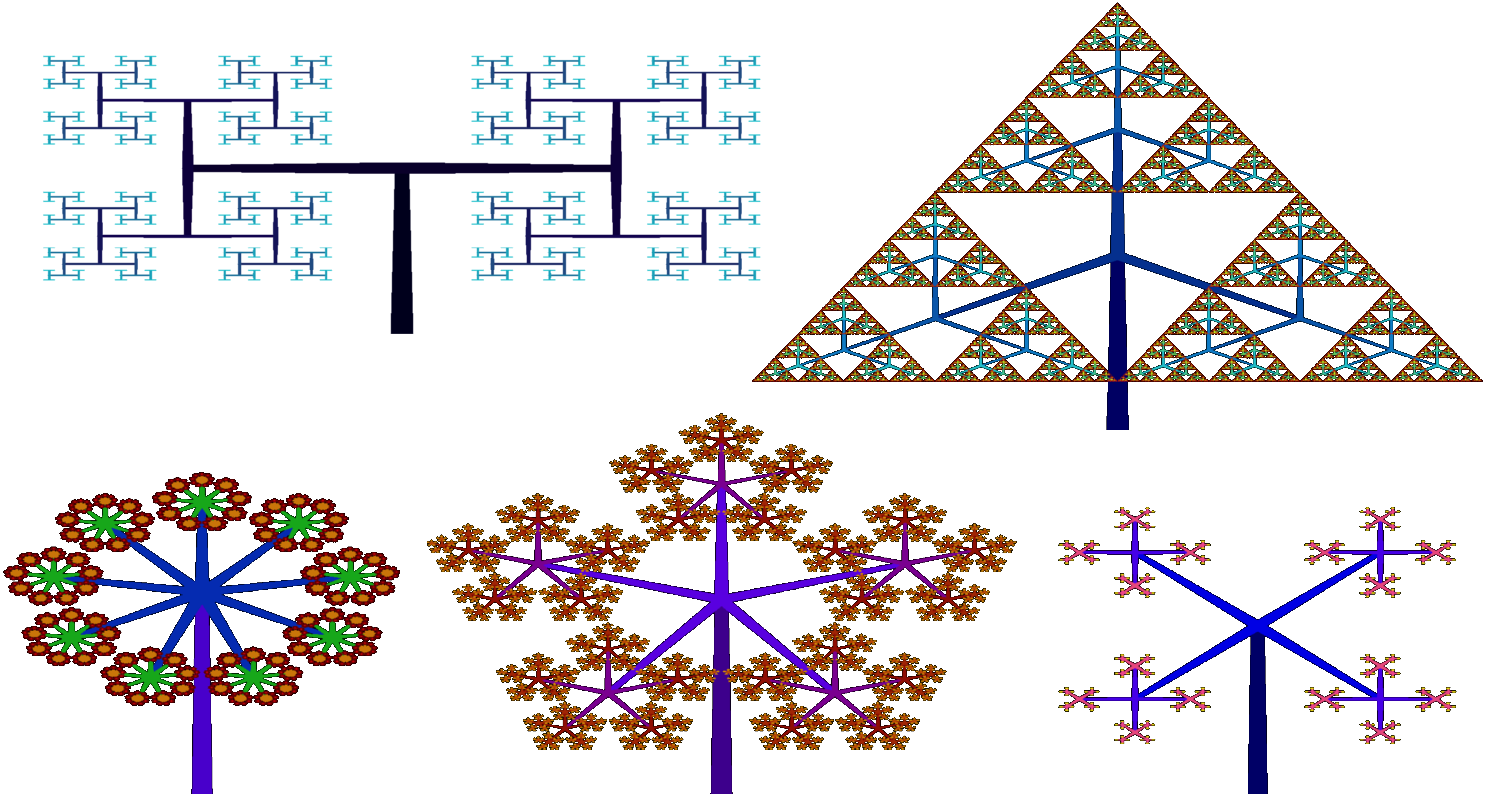
Fig. 2 - Going clockwise and starting at the top left, the number of branches to generate at a new node is 2, 3, 4, 5, and 9. The trunk length and branch ratio relative to the trunk have been adjusted to get a decent picture (hence why GUI widgets are wonderful for this project).

The ability to increase the number of branches at a node significantly changes the structure of the fractal, e.g. see Fig. 2 which displays the unexpected generation of a Sierpinski triangle among others; this behavior was a huge surprise for me. See Fig. 3 for an example of a tree with 4 branches generated a every node; it resembles the previous post but much fuller. Note that the number of iterations needs to be monitored when tweaking the number of branches to generated, otherwise too many lines are drawn and the program unavoidably crashes.

Fig. 3 - The number of branches generated at each node is 4, and the fractal has been generated with a modest angle of approximately 100 degrees.

Random Tree Generator

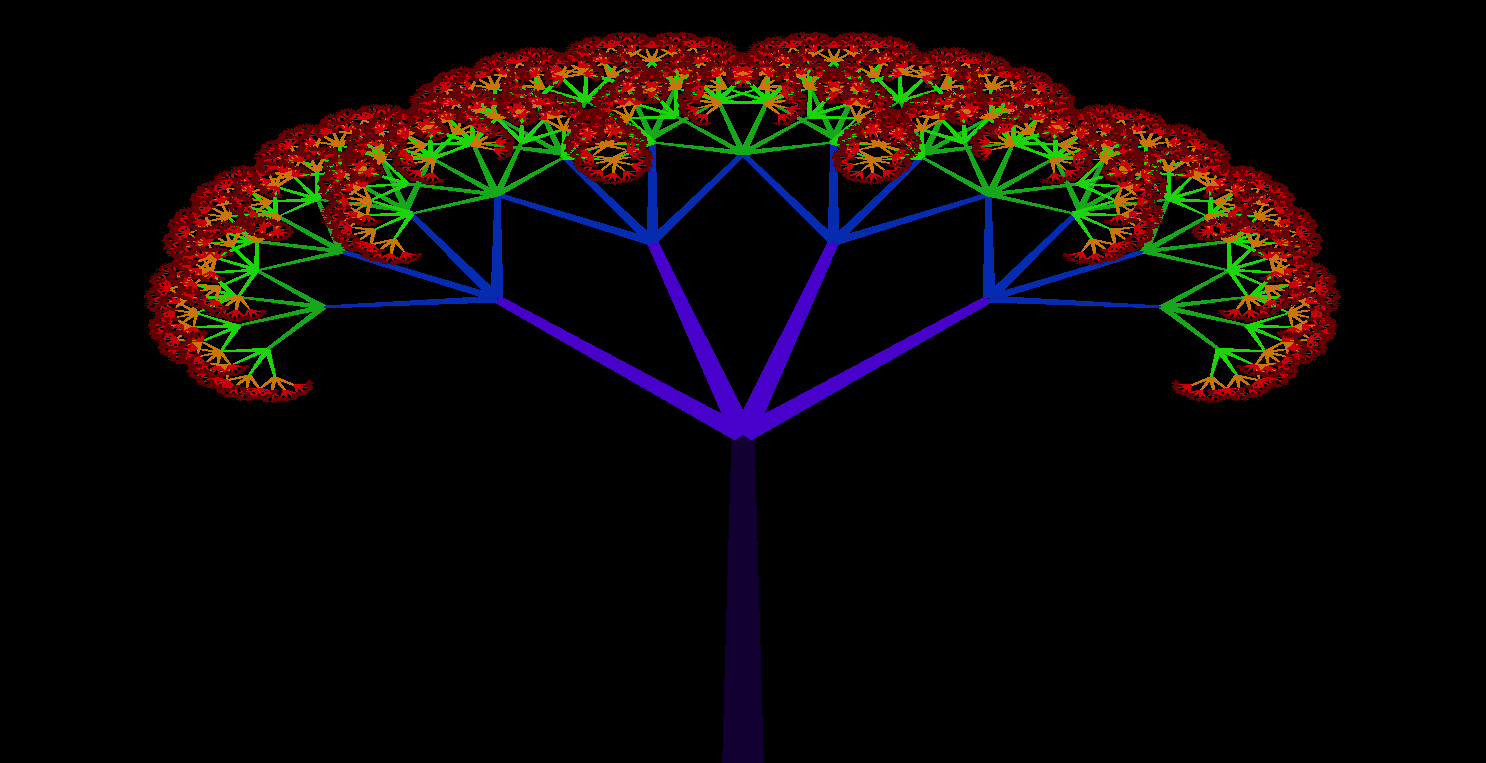
The random tree generator is useful for creating trees that visually look “natural” in structure, see Fig. 1. There are a great deal of parameters to randomize; however, this is what I did:

  1. change the number of branches to be generated at a particular node 10% of the time using a flat random generator - I do not want the change to be large, and I adjusted this number by +/- 1
  2. 10% of the time, change the length of the branch using a Gaussian distribution where the standard deviation is small, specifically 10% of the length of the branches that would normally be generated
  3. 33.3% of the time, change the generation angle with a Gaussian distribution of standard deviation equal to 10 degrees
  4. change the branch starting position with a Gaussian distribution (std dev = 10% of the normal branch length, and we must take an absolute value to avoid strange behavior) 40% of the time

These parameters can all be changed, obviously, but too many changes yields wild results; therefore, it is best to control how often a Gaussian (or flat) wiggle occurs. See the figures below for examples of the random generator with various options turned ON/OFF.

Examples

-->